

Example 2: Another man pushes a crate as shown with a force of 550 N and soes 2.2 kJ of work. Calculate the amount of work done by the man. Example 1: A man applies a force of 700 N to a crate and pushes it through a distance of 200 cm. To calculate the work required to compress the spring from ?30? cm to ?25? cm, we pretend that the spring ends at the origin, which means that compressing it to ?25? cm means we’ve compressed it to ?-5?, because ?25-30=-5?.īut we need to convert the units from cm to m, so the interval becomes ?0? m to ?-0.05? m. Work Done By a Constant Force & Energy Transfer. The work done to stretch a spring with natural length ?30? cm and spring constant ?k=500? from ?42? cm to ?48? cm is ?4.5? J. Stretching it to ?48? cm means we’ve stretched it from the origin to ?18?, because ?48-30=18?.īut we need to convert the units from cm to m, so the interval becomes ?0.12? m to ?0.18? m. To calculate the work required to stretch the spring from ?42? cm to ?48? cm, we pretend that the spring at its natural length of ?30? cm ends at the origin, which means that stretching it to ?42? cm means we’ve stretched it to ?12?, because ?42-30=12?.
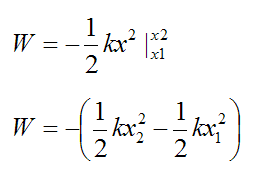
v the initial velocity of an object measured using m/s. vf the final velocity of an object measured using m/s. W the work done by an object measured using Joules. With ?k?, we can develop a generic equation for our spring using Hooke’s Law. Work done by an object can be scientifically expressed as: W 1 2 mvf2 - 1 2 mu2 Where, m the mass of the object measured using kilograms. Remember that we’ll be finding work in terms of Newtons and meters, which is why we converted ?10? cm to ?0.10? m. Since we know that a ?50? N force is required to stretch and hold the spring at a length of ?40? cm, from its natural length of ?30? cm, we’ll set ?F(x)=50? and ?x=0.10? m, which is the difference between the natural length and the stretched length, converted from cm to m. We’ll use Hooke’s Law to find ?F(x)?, but first we need to find ?k?. of 1 volt is applied o the ends of a conductor and I coulomb of electricity passes through. Work done by a Constant Force 1 J (Joule) 0.1020 kpm 2.778x10-7 kWh 2.389x10-4 kcal 0.7376 ft lbf 1 (kg m2)/s2 1 watt second 1 Nm 1 ft lb. How much work is done to compress the spring from ?30? cm to ?25? cm? From the definition of the volt (page 405), it follows that if a p.d. How much work is done to stretch the spring from ?42? cm to ?48? cm? A ?50? N force is required to stretch and hold the spring at a length of ?40? cm. When you know natural length and the force required to stretch the springĪ spring has a natural length of ?30? cm.


 0 kommentar(er)
0 kommentar(er)
